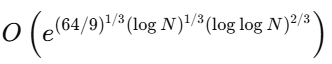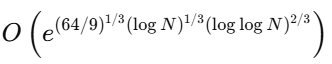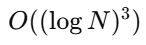The Complexity of Quantum Algorithms: Unraveling the Mystery

The Complexity of Quantum Algorithms: Unraveling the Mystery

Quantum computing often feels like stepping into a science fiction narrative, where particles can exist in multiple states simultaneously and entanglement creates mind-bending correlations. At the heart of this field are quantum algorithms—methods designed to leverage these unique properties of quantum systems to solve problems faster than classical computers. However, understanding the complexity of quantum algorithms requires a careful look at how they differ from their classical counterparts and how we evaluate their efficiency.

What Makes Quantum Algorithms Special?

Quantum algorithms operate in a realm where information is processed using qubits instead of classical bits. Unlike bits, which are strictly 0 or 1, qubits can exist in superpositions, representing multiple states simultaneously. This allows quantum computers to explore many possibilities at once. Additionally, quantum entanglement enables qubits to share information in ways classical systems cannot, allowing certain problems to be solved with fewer steps.

These unique features suggest that quantum algorithms can tackle specific problems exponentially faster than classical algorithms. However, this advantage does not apply to all problems. Understanding their complexity requires dissecting not only how they work but also how they are analyzed.

Complexity Measures in Quantum Algorithms

The complexity of an algorithm refers to the resources it uses—typically measured in terms of time (how long it takes) and space (how much memory it requires). In quantum computing, time complexity is often the focus, and the number of quantum gates required to execute the algorithm plays a critical role.

For example, Shor’s Algorithm, which revolutionized cryptography, is designed to factor large integers exponentially faster than classical algorithms. Classical factoring algorithms, like the best-known general number field sieve, have a complexity of approximately

In contrast, Shor’s Algorithm achieves a quantum complexity of

a dramatic reduction for sufficiently large N.

Another landmark is Grover’s Algorithm, used for unstructured search problems. While classical search algorithms require O(N) operations to search a list of N items, Grover’s Algorithm achieves this in O(√N)steps. Though this is not an exponential improvement, it is significant for large datasets.

Quantum algorithms for simulating physical systems, such as the Quantum Phase Estimation Algorithm, are central to quantum chemistry and material science. They provide exponential speedups for certain problems in simulating quantum systems, outperforming classical approaches that scale poorly due to the exponential growth of the state space.

Classical vs. Quantum Complexity

The comparison between classical and quantum complexity reveals stark differences in certain domains but also highlights that quantum advantages are not universal. For instance, sorting algorithms such as quicksort or mergesort operate in O(N log N) time classically. While quantum computing does not currently offer a better general-purpose sorting algorithm, specialized tasks like structured search see clear quantum benefits.

In cryptography, the implications are dramatic. Problems like factoring and discrete logarithms underpin classical encryption systems, which are rendered insecure by quantum algorithms like Shor’s. Yet, some problems, such as those used in lattice-based cryptography, are believed to resist quantum attacks, showcasing that quantum supremacy has its limits.

Estimating Complexity: Quantum vs. Classical

In classical algorithms, complexity is often estimated by counting the number of elementary operations, such as additions or comparisons. The computational model is well-defined, and benchmarks are based on realistic hardware constraints.

For quantum algorithms, the process is more nuanced. Complexity is estimated in terms of quantum gates—the fundamental operations that manipulate qubits. Since quantum operations are inherently probabilistic, complexity often includes the cost of achieving sufficient accuracy. Algorithms must be repeated multiple times to reduce error probabilities, adding another layer of complexity to the analysis.

Moreover, quantum algorithms must contend with decoherence and noise, which degrade performance over time. This makes practical complexity estimates dependent on the quality of the quantum hardware, such as gate fidelity and coherence times. These factors are absent in classical complexity measures, making quantum complexity inherently more complex to evaluate.

The Road Ahead for Quantum Algorithms

The complexity of quantum algorithms continues to intrigue researchers. Algorithms like Shor’s and Grover’s have set a benchmark, but the field is far from reaching its full potential. The challenge lies not only in developing new algorithms but also in refining quantum hardware to realize their theoretical speedups.

For now, quantum computing excels in solving specific problems that are intractable for classical systems. However, as quantum technology matures, we may uncover new algorithms that redefine what is computationally feasible, reshaping fields from cryptography to drug discovery.

Conclusion: Complexity as the Key to Progress

Understanding the complexity of quantum algorithms is essential for grasping their power and limitations. By comparing them with classical counterparts and exploring how they are analyzed, we see how quantum computing can revolutionize problem-solving in certain domains. While challenges remain, the progress made so far highlights the potential of quantum algorithms to tackle problems that classical systems can only dream of addressing. The journey is just beginning, and complexity will remain at the heart of unlocking quantum computing’s full promise.

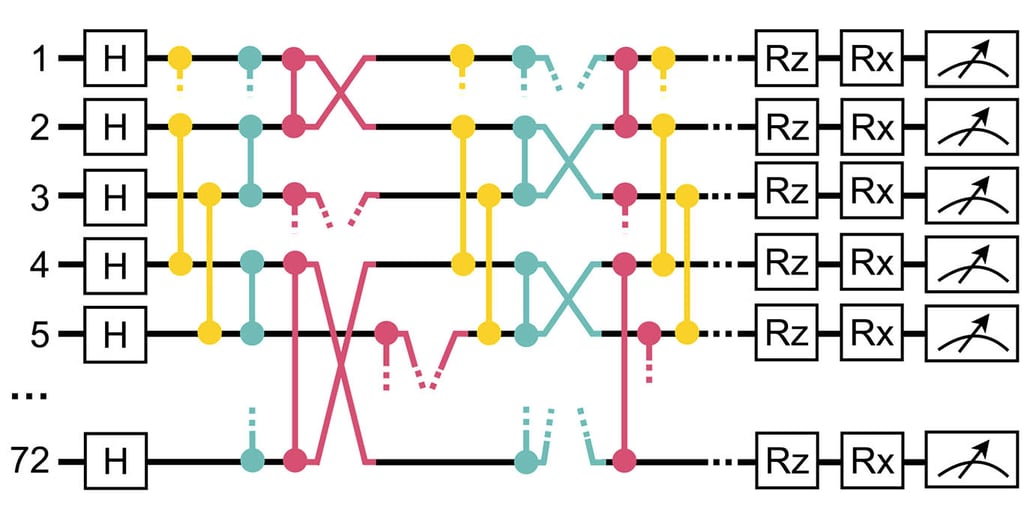
Image Courtesy: Quantum Computing Report, https://quantumcomputingreport.com/quantum-technology-algorithm-trends-tidying-up